Hmmm..., por dónde empiezo...
Esto es demasiado complejo así que intentaré ir por partes simplificándolo lo más que pueda, describiendo primero lo que he observado en la estructura de los sistemas musicales regulares y sus escalas musicales y después lo intentaré de ir demostrando de forma sencilla. He hecho un video en Youtube sobre esto también que puedes ver aquí, pero aquí en el blog está mejor explicado.
Lo que he observado parece indicar que lo que genera todo esto que se va a ver aquí, es o está relacionado con un hipercubo, más concretamente con la figura vértice de un hipercubo (es decir, en cuatro dimensiones geométricas creo que sería un pentacoron, siendo su equivalente en tres dimensiones el tetraedro), aunque no puedo afirmarlo al cien por cien porque cuanto más se profundiza en esto, tanto más se multiplica la complejidad (y en vez de ser un pentacoron podría ser un 16-cell, siendo su equivalente en tres dimensiones el octaedro, es difícil asegurarlo, ya que comparten matrices secuenciales, supongo que por ser de la familia de los politopos regulares, pero vamos que todo apunta a que lo que genera todo esto es la figura vértice de un hipercubo de n-dimensiones, pero no de forma aislada sino que depende de este último, es decir, esta estructura parece estar como "enganchada" a un hipercubo, se que suena extraño pero es lo que es, todo apunta a ello). Lo que sí es seguro es que lo que se va a ver aquí sobre música está relacionado con geometría, sobre todo con la familia de los politopos regulares convexos n-dimensionales. En cuatro dimensiones geométricas hay 6 politopos regulares y a partir de la quinta dimensión geométrica solo hay 3 de estos, así que es algo importante a tener en cuenta, porque n-dimensional quiere decir infinitas dimensiones, es decir, solo puede ser o un tetraedro o un cubo o un octaedro o la conjugación de estos o uno inscrito dentro del otro (o alguno de estos tres y la intervención de un cuarto desconocido, pudiendo ser este cuarto una especie de malla que cruce o intersecte un hipercubo y cree así la figura vértice o pentacoron que nos ocupa en esta observación, o que otro politopo regular n-dimensional se acople a un hipercubo, pudiendo ser otro hipercubo, creando así esta figura vértice u otras posibilidades que estoy abierto a conjeturar). Y si queremos echarle imaginación, si esto estuviera "vivo" y se moviera delante nuestra, haría algo así parecido a este duocilindro o a este teseracto o hipercubo de cuatro dimensiones o a este pentácoron o 5-cell.
Bueno, empecemos.
El orden de las escalas describen las secuencias de vértices y aristas de un Hipercubo n-dimensional
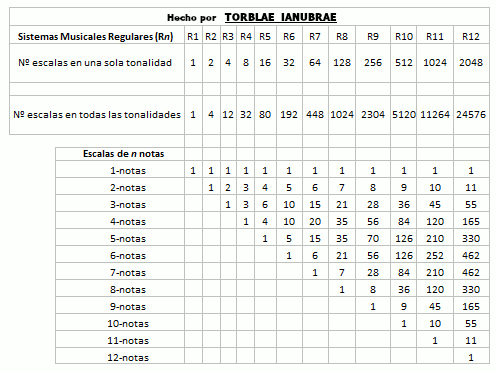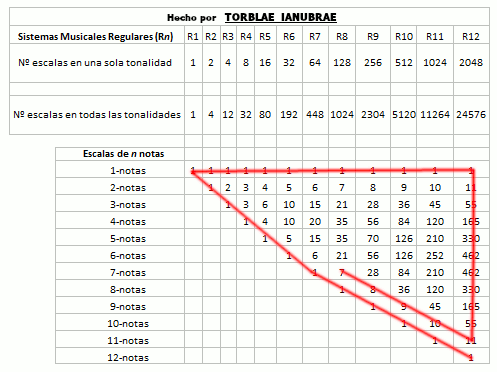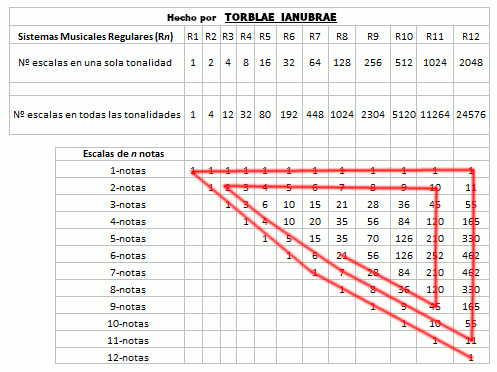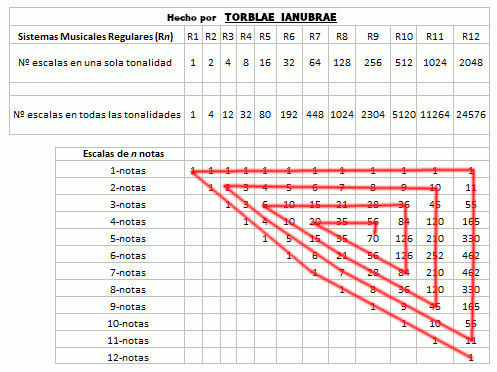
El total de escalas en orden en todas las tonalidades posibles de los que he dado en llamar sistemas musicales regulares (1, 4, 12 ,32, 80, 192, 448, 1024, 2304, 5120, 11264, 24576, ...) calzan exactamente con la secuencia de las partes (aristas) de un hipercubo n-dimensional. Al mismo tiempo, el total de escalas en orden en una sola tonalidad de los que he dado en llamar sistemas musicales regulares (1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048, ...), calzan exactamente con la secuencia de los vértices de un hipercubo n-dimensional. La cosa no para aquí, sino que se hace más compleja.
A continuación se muestra la tabla de Elementos Hipercubicos, la cual está describiendo formas geométricas relacionadas con el cubo desde la dimensión geométrica 0 hasta la 10, pudiendo continuar hasta infinitas dimensiones geométricas si así se quisiera:
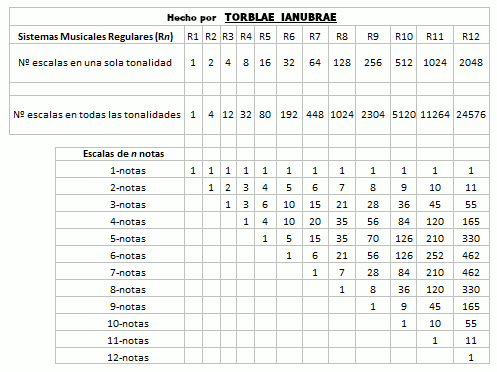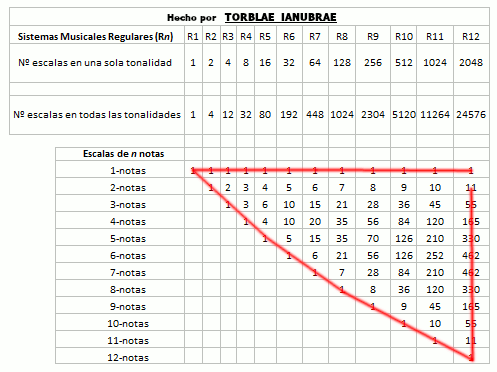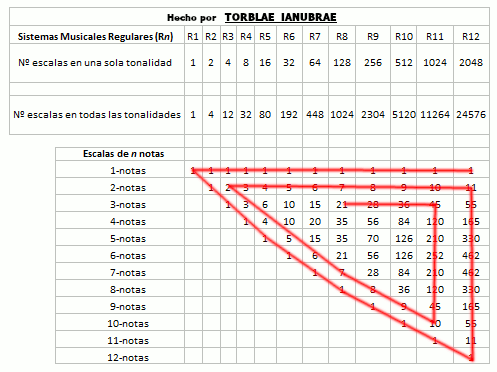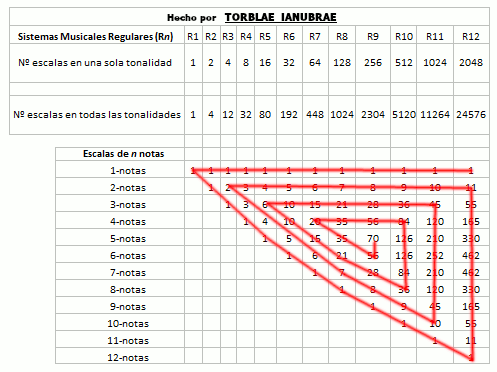
Nótese en la imagen anterior como la secuencia de la columna Vértices 0-caras es igual a la secuencia del número de escalas en una tonalidad en los sistemas musicales regulares y que la secuencia de la columna Aristas 1-caras es igual a la del número de escalas en todas las tonalidades en los sistemas musicales regulares, que se mostrará en la siguiente tabla. He acotado los sistemas musicales regulares hasta el 12 por cuestión de espacio, pero podría continuar hasta infinito (y también lo he acotado a doce porque en este sistema o matriz que se genera, al parecer el 12 es como un punto de equilibrio, pero no lo puedo asegurar con total certeza porque tengo que observarlo e investigarlo más a fondo). La siguiente imagen se puede leer por columna así: el Sistema Musical Regular R12 (Temperamento Igual) tiene 2048 escalas en una sola tonalidad y 24576 escalas en todas sus tonalidades y tiene (en una sola tonalidad) 1 escala de una nota, 11 escalas de dos notas, 55 escalas de tres notas, 165 escalas de cuatro notas, etcétera. :
Triángulo de Pascal (Pingala-Khayyam-Yang Hui)
Si ordenamos las escalas (en una sola tonalidad) de los que he dado en llamar sistemas musicales regulares mediante el proceso que he dado en llamar escalas derivadas o método de derivación, vemos que calzan exactamente con lo que en occidente se conoce como Triángulo de Pascal (de hecho, es posible que esto sea lo que crea al llamado Triángulo de Pascal, que dicho "triángulo" era ya conocido por el indio Pingala en el 200 a.C., por el persa Khayyam sobre el 1100 d.C. y por el chino Yang Hui sobre el 1270 d.C. y después algunos más). Por si no se ve claro en la imagen anterior, pondré otra imagen:
En esta imagen anterior el Triangulo de Pascal se forma de manera que los matemáticos llaman del tipo matriz simétrica de Pascal. Y bueno, este triángulo y algunas de las propiedades matemáticas que encierra son algo conocidas (como los coeficientes binomiales de Pascal, la Pirámide de Pascal, los Pascal's simplex, también es de donde viene el Triángulo armónico de Leibniz, y más cosas curiosas como que en el se esconde el número PI, el número e, números naturales, números triangulares, números tetraédricos, números pentatopicos y 6-simplex 7-simplex y así hasta números n-simplex infinitos, números cuadrados perfectos, números poligonales, triángulo de Sierpinski, la sucesión de Fibonacci, los puntos en un circulo que va dibujando figuras geométricas, etc.). Pero como yo estoy mostrando la correlación de todo esto con las escalas musicales, lo siguiente que vamos a ver es que también está mostrando algo muy importante en música, que es la serie armónica, en la que se han inspirado en algo más de 2000 años de historia, docenas si no centenas de diversos tipos de sistemas musicales irregulares, como yo les he dado en llamar por no tener todos sus intervalos iguales, como el Pitagórico, el de Justa Entonación, Mesotónicos, etcétera, todos ellos basándose en la simple relación de ir dividiendo una cuerda a su mitad.
Y aquí está la serie armónica, tanto en la imagen anterior como en la siguiente (en esta ultima se divide el número de arriba por el de abajo):
Pero esto no es todo. La complejidad de esta estructura de los que yo llamo sistemas musicales regulares y de sus escalas continúa, porque lo que se está mostrando en la imagen anterior, lo está haciendo con las escalas posibles de estos sistemas musicales regulares en una sola tonalidad. Para hallar el siguiente Triángulo (aclaro que no por capricho sino porque así se construye este sistema, yo me limito a observarlo y a estudiar su estructura siguiendo la lógica del mismo) sólo hay que ir multiplicando los números de estas escalas posibles en una tonalidad por el número del sistema musical regular que las genera, así nos daría el número total de escalas que son posibles en todas las tonalidades posibles de ese sistema musical regular en particular (mostrándonos de este modo donde estará el límite para generar triángulos de este tipo). Es muy sencillo:
R1 * 1 = 1
R2 * 1 = 2 , R2 * 1 = 2
R3 * 1 = 3 , R3* 2 = 6 , R3 * 1 = 3
R4 * 1 = 4 , R4 * 3 = 12 , R4 * 3 = 12 , R4 * 1 = 4
...
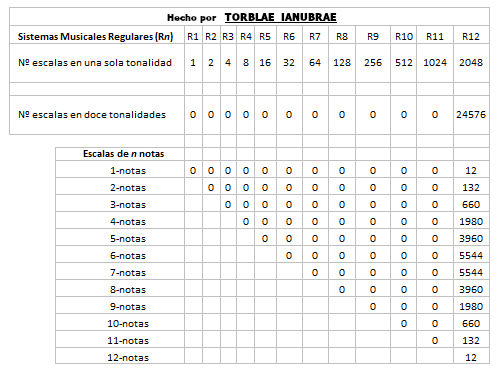
Al hacer el paso anterior hallaremos un siguiente triángulo en perfecta sintonía con todo esto que estamos viendo, porque está guardando la proporción dada desde un principio, es decir, con los hipercubos de n-dimensiones y demostrando el límite. Se entenderá mejor si hacemos la pregunta siguiente: ¿Cuántas escalas en total, en todas sus tonalidades posibles, tiene un sistema musical regular de 1 nota (R1)? ¿Cuántas escalas en total, en todas sus tonalidades posibles, tiene un sistema musical regular de 2 notas (R2)? ¿Y uno de 3? ¿Y uno de 4? ¿Y uno de n notas?
Como vamos a ver después, esto se va a ir haciendo algo más complejo, así que voy a ir poniendo nombre a este nuevo triángulo de la imagen anterior y le llamaré Triángulo Delimitador, porque hace precisamente eso, marcar el límite máximo de escalas en todas las tonalidades que estos sistemas musicales regulares tienen (en este caso elegimos previamente doce sistemas musicales regulares, pues entonces el Triángulo Delimitador mostrará todas las escalas posibles de todos estos doce primeros sistemas musicales, pero podrían ser los primeros 30 o 999 o los que queramos hasta infinito). Este sería al que llamo Triángulo Delimitador (y recuerda que estamos aplicando la lógica de este sistema, no la lógica del Triángulo de Pascal, ya que este último se ha generado con la lógica de este sistema):
Este triángulo, al estar ligado al anterior (es decir al llamado Triángulo de Pascal) podría esconder ciertas propiedades matemáticas en él. Por ejemplo, así a primera vista uno puede ver la secuencia de los números oblongos. En la siguiente imagen se verá mejor:
Algunos dirán que es casualidad, que son números al azar y que si algo significan eso es puro caos determinista. Yo digo que le demos a este Triángulo Delimitador (y a los demás que vamos a ir viendo) los 368 años que tiene el Triángulo de Pascal, para que puedan ser estudiados del mismo modo y si en esos 368 años no se encuentra nada en ellos, entonces se podrá afirmar que estos otros triángulos (que se generan de la misma forma que el de Pascal) no tienen las mismas propiedades, aunque que aparezca la sucesión de números oblongos ya viene siendo indicativo de que sí que las tienen, no necesariamente las mismas sino que puede que diferentes. Para ser justos, hay que dar esos 368 años a este Triángulo Delimitador y a los demás triángulos que vamos a ir viendo, para que puedan ser estudiados del mismo modo que lo ha sido el de Pascal.
A los ingenieros en informática e ingeniería de computadoras les encantarán estos nuevos triángulos y saber de dónde vienen, para hacer sus arrays binarios o lo que tengan que hacer. Es bastante posible que ya los conozcan por haber calculado binomios o arrays con el Triángulo de Pascal, pero es posible también que los que muestre en estos siguientes triángulos no los conozcan, porque el Triángulo de Pascal que mostré antes sigue su propia lógica. Así que para diferenciar ambos, como son exactamente iguales, al Triángulo de Pascal que nos apareció antes le llamaré Triángulo Unitonal (ya que se deduce por ordenar todas las escalas posibles en una tonalidad de todos los sistemas musicales regulares posibles, por esto lo de Unitonal). Voy a poner un ejemplo rápido del por qué es necesario que haga esta distinción. Un Triángulo de Pascal lo suelen construir así:
1
1, 1
1, 2, 1
1, 3, 3, 1
1, 4, 6, 4, 1
1, 5, 10, 10, 5, 1
Lo que sucede es que he encontrado esta sucesión en la OEIS, la A028326 y por lo que se puede ver allí, lo que hacen es multiplicar el anterior Triángulo de Pascal por 2, así:
2
2, 2
2, 4, 2
2, 6, 6, 2
2, 8, 12, 8, 2
2, 10, 20, 20, 10, 2
Y como vamos a ver en un momento, el desarrollo del Triángulo Unitonal (recuerda que me refiero al primero que mostré, el que generaba el Triángulo de Pascal) sigue una lógica diferente y se genera por ordenar todas las escalas musicales de todos los sistemas musicales que yo llamo regulares, desde uno hasta infinito, a través del método que he dado en llamar método de derivación o escalas derivadas, que puede aplicarse a cualquier sistema musical para deducir de su escala cromática cuántas escalas son posibles en ese sistema musical en particular, obteniendo de más a menos escalas, por ejemplo, en un sistema de doce notas musicales se obtendrían escalas de once notas, después de diez, después de nueve y así hasta su límite mínimo que sería de una.
Bueno, continuemos ahora con el siguiente triángulo que podemos sacar con este ordenamiento de escalas de los sistemas musicales regulares en orden. No entraña mucha dificultad pero sí que es algo más complejo que antes. Recordemos que en el primer recuadro donde se generaba el Triángulo Unitonal estaba mostrando el número de escalas en una sola tonalidad de todos los sistemas musicales regulares posibles y que este último recuadro que hemos visto, donde se genera el que he llamado Triángulo Delimitador, estaba mostrando el número de escalas de todos los sistemas musicales regulares posibles en todas las tonalidades. Lo he hecho en este orden para demostrar que tiene un inicio y un límite lógicos, de hecho, me estoy basando en cómo se generan escalas en un sistema musical regular y por lógica, un sistema musical regular tiene su nota inicial y su nota final que generan una escala cromática, así que no tiene dificultad alguna (la propia lógica del sistema señala dónde está el comienzo y dónde el final en el Triángulo Delimitador). Ahora bien, lo que esta lógica nos va a dar, van a ser nuevos triángulos como el Unitonal (recuerda que este genera exactamente el Triángulo de Pascal) y el Delimitador, porque hemos visto las escalas que un sistema musical regular tiene en una tonalidad y en todas, ¿pero cuántas escalas totales tienen estos sistemas musicales regulares si les acotamos en dos tonalidades, en tres, en cuatro, en cinco, en n, hasta su límite de notas? Esto es difícil de ver a primera vista, pero voy a poner un ejemplo con la propia lógica de este sistema.
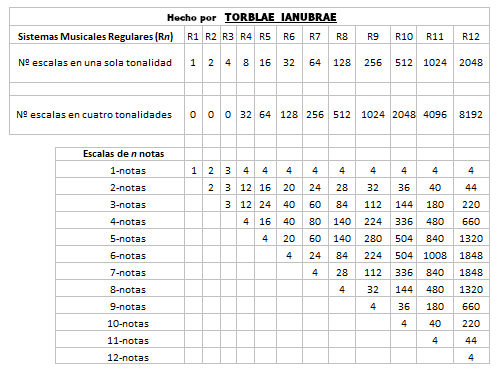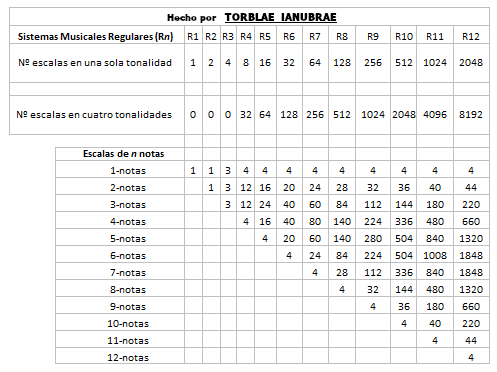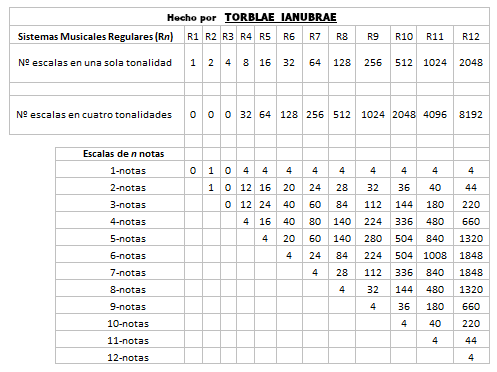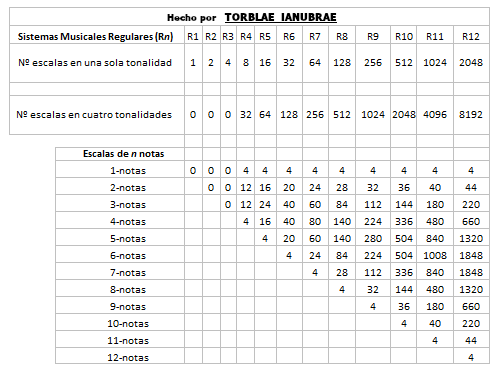
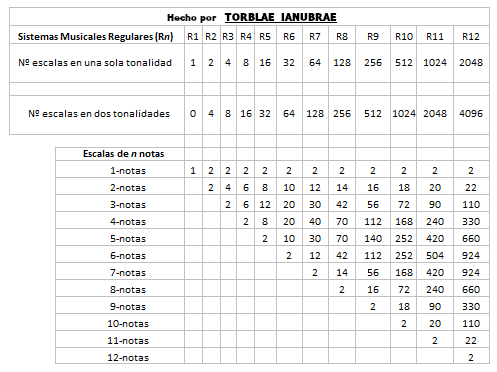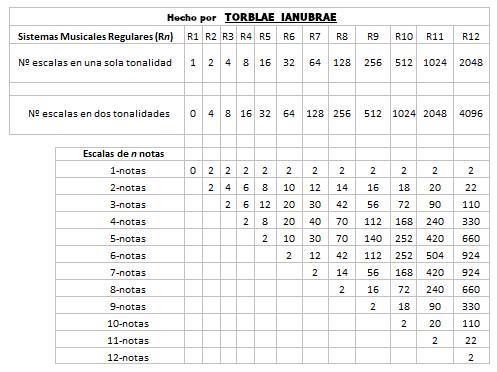
Elijamos al R12 (Temperamento Igual). Si te digo que de las doce tonalidades que tiene este sistema musical toques la escala mayor en sólo dos tonalidades y tu eliges la tonalidad de DO y la tonalidad de MI, estamos acotando todas sus tonalidades posibles solo a dos de ellas. ¿Cuántas escalas posibles de una nota, de dos, de tres y así hasta doce, tendrías para tocar con estas dos tonalidades de este sistema musical R12? Si quieres saber la respuesta, observa la columna del R12 en el siguiente cuadro, donde se muestran también todas las posibilidades en dos tonalidades de todos los otros primeros once sistemas musicales regulares y pudiendo continuar todas estas secuencias hacia su derecha y abajo hasta infinito, en infinitos sistemas musicales regulares de infinitas notas:
A este nuevo triángulo de la imagen anterior le vamos a llamar Triángulo Bitonal (porque lo hemos creado a partir de sólo seleccionar dos tonalidades en un rango de los doce primeros sistemas musicales regulares). Y como se puede apreciar en la imagen anterior, ahí está la diferencia entre el Triángulo Bitonal con el Triángulo de Pascal multiplicado por dos. Si echamos de nuevo un vistazo al Triángulo de Pascal multiplicado por dos, veremos que empieza por 2:
2
2, 2
2, 4, 2
2, 6, 6, 2
2, 8, 12, 8, 2
2, 10, 20, 20, 10, 2
Y si miramos el Triángulo Bitonal de la imagen anterior, veremos que empieza por cero. ¿Por qué? Pues por la lógica de este mismo sistema. La siguiente pregunta te lo aclarará. ¿Cuántas escalas de dos tonalidades diferentes puedes tocar con un sistema musical de una sola nota? Cero.
Justo aquí, antes de continuar con el siguiente triángulo que se creará al acotar todos los sistemas musicales sólo a tres tonalidades, puede ser que suceda algo de extrema complejidad, que merece ser observado o al menos empezar a tenerlo en cuenta como una posibilidad. Después comentaré de qué se trata, pero adelantaré aquí que puede que sea posible que la verdadera naturaleza de este cero del Triángulo Bitonal en realidad se esté moviendo del 0 al 1 y de vuelta al 0 y otra vez al 1 y así, intentando llegar a las dos tonalidades propuestas, buscando estabilizarse, por decirlo de alguna manera.
Veamos ahora cuántas escalas totales tienen estos sistemas musicales regulares si les acotamos en tres tonalidades y el triángulo que genera, al que llamaremos Triángulo Tritonal:
Este Triángulo Tritonal, como se puede apreciar en la imagen anterior, empieza por cero y le siguen otros dos ceros. ¿Por qué? Pues por la lógica de este mismo sistema. ¿Cuántas escalas de tres tonalidades diferentes puedes tocar con un sistema musical de una sola nota? Cero. ¿Y cuántas escalas de tres tonalidades diferentes puedes tocar con un sistema musical de dos notas? Cero.
Voy a ir mostrando ahora los demás triángulos que irían apareciendo para demostrar y aclarar más la lógica de este sistema y pararé en el 12 (no sólo por cuestión de espacio en la imagen sino también por lo que comenté antes, que parece ser que el 12 actúa como un punto de equilibrio entre todos los demás sistemas musicales regulares, pero necesito observarlo mejor aunque de todas formas mostraré después a qué me refiero exactamente). Veamos ahora cómo continúan los demás triángulos.
Así es el Triángulo Tetratonal:
Así es el Triángulo Pentatonal:
Así es el Triángulo Hexatonal:
Así es el Triángulo Eneatonal:
Así es el Triángulo Decatonal:
Así es el Triángulo Endecatonal:
Y así es el Triángulo Dodecatonal:
Voy a intentar mostrar ahora con unas imágenes a que me refería antes con que se tuviera en cuenta la posibilidad de que quizá la verdadera naturaleza de esto, cuando limitamos el número de tonalidades, sea que los ceros se muevan como intentando llegar a una tonalidad que no puede, intentando estabilizarse. Esta primera imagen mostrará qué podría pasar en el llamado Triángulo Bitonal (nótese que el cero y el uno podría ser los dos al mismo tiempo o por el contrario que se mueva tan rápido que aparenta ser ambos, pero en realidad lo que intenta es estabilizarse):
En esta siguiente imagen se mostrará lo que podría estar pasando en el Triángulo Tritonal:
Y esta otra imagen muestra lo que podría estar pasando en el Triángulo Tetratonal:
Y así podríamos continuar hasta infinito pero no lo haré porque es mucho trabajo hacer todas estas combinaciones en imágenes (parece ser que sigue una secuencia, 2,6,12,20,30, ..., la de los números oblongos y también la lista de posibles diagonales de un poliedro convexo de n caras) y con estos tres ejemplos de estas tres ultimas imágenes ya se entiende la lógica que podría tener todo este sistema. Puede que este loco o que esto suene muy extraño a muchos pero, cuanto más observo esto más me convenzo de que es, simplificándolo, un tetraedro que está dentro de un cubo y el cubo lo que hace es limitar al tetraedro, pero al mismo tiempo que lo limita lo estabiliza, así que el tetraedro puede expandirse o contraerse tanto como quiera porque será estable gracias al hipercubo que lo contiene (y al núcleo del tetraedro que podría decirse que es un octaedro). Y además puede expandirse o contraerse por tantas dimensiones geométricas como quiera, porque tanto el tetraedro como el cubo son dos de los tres únicos politopos regulares convexos que están presentes desde la quinta dimensión geométrica en adelante (el tercero "casualmente" es el octaedro).
A continuación mostraré diversos tipos en los que este sistema puede expandirse y contraerse.
Esta siguiente imagen es la expansión que llamo linear en el Triángulo Unitonal (el que genera el Triángulo de Pascal). Empieza en el sistema musical regular R1, recorre su escala y pasa al R2, recorre sus escalas de menos a mas y pasa al R3, recorre sus escalas de menos a mas y pasa al R4, recorre sus escalas de menos a mas y...etcétera (nótese que a la inversa se contrae y que hay mas tipos posibles de expansión y contracción):
La siguiente imagen muestra la que llamo expansión ondular (sucede lo mismo que con la linear):
La siguiente imagen muestra la que llamo expansión espiral (sucede lo mismo que con las dos anteriores):
A continuación una expansión-contracción hibrida (secuencia Fibonacci), como un pulsar, se expande y contrae (no tiene la secuencia de Fibonacci completa porque se ha acotado solo a doce sistemas musicales regulares):
Ahora pondré unas imágenes más que son interesantes por como se expande y contrae en espiral.
A esta siguiente imagen la llamo 1ª expansión del Triángulo Unitonal (en sus vértices se generan unas secuencias), nótese que primero se expande hasta llegar a un límite dado de sistemas musicales regulares (Rn), en este caso doce pero puede ser infinito, y recorre todas las escalas de una nota de estos doce primeros sistemas musicales regulares en una sola tonalidad, después cuando llega al limite dado de sistemas musicales regulares, que es doce en este caso, aunque parezca que está descendiendo, en realidad está ascendiendo, es decir, se expande ahora recorriendo el número total de escalas de una nota, de dos, de tres, etc., y después se contrae y repite este proceso de tres etapas (expansión, segunda expansión y contracción):
Un programador o ingeniero de computadoras verá en la imagen anterior una especie de array, y eso está bien, pero tiene que darse cuenta que este sistema lógico, esta estructura, es bastante más compleja que eso. Recordemos que puede ser posible que al acotar las tonalidades de estos sistemas musicales a menos de las que pueden, al no llegar a ellas, podrían intentarlo de todos modos buscando estabilizarse. Intentaré poner un ejemplo. Digamos que un computador hace lo que se mostró en el Triángulo Bitonal, es decir, se mueve en ceros y unos, así:
Como ya se dijo antes, podemos ver esto como que el cero y el uno podría ser los dos al mismo tiempo o por el contrario que se mueva tan rápido que aparenta ser ambos, pero en realidad lo que intenta es estabilizarse (porque su naturaleza, su esencia más pura le empuja a ello, como las partículas, algo las empuja a comportarse del modo en que lo hacen). Podríamos decir entonces que podría tener dos naturalezas, la primera es que sea cero por un lado y uno por otro, lo que vendría a ser el sistema binario en informática clásica. Su segunda naturaleza es que podría ser el cero por un lado, el uno por otro y el cero y el uno al mismo tiempo por otro (algo que se podría descomponer en que puede ser cero y uno y cero cero y cero uno), lo que vendría a ser un qubit en informática cuántica. Pero este sistema, esta estructura, es mucho más compleja y es normal que así sea, porque estamos observando la capacidad de la naturaleza. El siguiente triángulo a este anterior, es el Triángulo Tritonal, y este nos muestra que la complejidad aumenta al expandirse:
Lo que describiría ahora esta imagen anterior sería un qutrit cuántico, algo por encima del qubit, ya que ahora el estado de las escalas en R2 puede ser 0 y 1 y 2. Y así la complejidad aumentaría cuanto más se expande, es por eso que si un informático quiere ver esto como un simple array pues está bien para simplificarlo, pero podría ser mucho más complejo que eso, como acabamos de ver.
Veamos ahora a lo que llamo 1ª contracción del Triángulo Tritonal, y pondré las imágenes seguidas para que se vea como son, porque se está alargando mucho este post y aún quedan algunas cosas mas por explicar:
Esta es la 2ª expansión del Triángulo Unitonal:
Esta es la 2ª contracción del Triángulo Unitonal:
Esta es la 3ª expansión del Triángulo Unitonal:
Y esta ultima, es la que llamo 3ª contracción del Triángulo Unitonal:
Insisto, hay que tener en cuenta que el comportamiento de esto podría ser mucho más complejo. Yo estoy simplificando todo esto que tengo en mi cabeza lo más que puedo para que se comprenda y digamos que muestro fotografías o sucesos estáticos de la estructura de este sistema que dibujan las escalas musicales de sistemas musicales regulares. Pero imaginemos, barajemos la posibilidad de que no sea una fotografía o suceso estático estable, sino algo en movimiento o sucesos dinámicos, podríamos imaginar entonces en la imagen anterior que sólo al sistema musical regular R8 se le aplica lo de acotar sus tonalidades a solo seis de ellas por ejemplo (mientras el resto de sistemas musicales regulares se quedan "estables" en una sola tonalidad), estarían entonces parpadeando todas las escalas del R8 del 0 al 6, haciendo montones de combinaciones entre ellas y las de los demás sistemas musicales. Y no solo eso, imaginemos ahora que mientras está sucediendo esto anterior, al sistema musical regular R5 se le acotan sus tonalidades a 3, mientras el R8 vuelve a tener todas sus tonalidades y sus escalas quedan estables de nuevo en una sola tonalidad, pero el R11 ahora acota sus tonalidades a 9, es decir todas sus escalas parpadearían del 0 al 9, y de repente el R11 cambia a tener sus tonalidades acotadas a 7 y entonces el R2 el R3 y el R12 acotan sus tonalidades a 5. ¿Se entiende ahora? No digo que sea así, pero podría ser así de complejo en realidad, es una cuestión que no descarto. A ver, lo que sucedía en el Triángulo Bitonal, ese 0 y 1 parpadeantes en el R1, que podríamos llamar ahora suceso dinámico de rango 1, es bastante equiparable a lo que sucede en computación clásica y cuántica, y la computación cuántica digamos que estudia cómo manejar las partículas mediante los qubits. Si se tuvieran computadoras cuánticas, la forma de mejorarlas sería manejando las partículas mediante qutrits, que es equiparable a lo que sucede en el Triángulo Tritonal, ese 0 y 1 y 2 parpadeantes en R2 y el 0 y el 1 parpadeantes en R1, que podríamos llamar ahora sucesos dinámicos de rango 2. Un computador cuántico podría manejar qutrits con algunos truquillos, pero no tan bien o no con la misma facilidad en que lo haría un computador cuántico que maneje qutrits (o sucesos dinámicos de rango 2). Sin embargo crear solo un computador cuántico (que maneje sucesos dinámicos de rango 1) ya es bastante complejo, al igual que programarlo también es muy complejo. ¿Y esto a qué viene? Pues que crear un computador cuántico que maneje sucesos dinámicos de rango 12 o 20 o 500 o más (como podría ser el verdadero comportamiento de esta estructura de las escalas musicales que estamos observando), está casi fuera del alcance de la capacidad humana, por no decir completamente. Solo es una conjetura que tengo como un simple observador que soy, conjetura que cualquier entendido en el tema podría echar abajo diciendo que sí, que echándole imaginación podría verse como equiparable lo que sucede en el Triángulo Bitonal con superposición cuántica, pero que en mecánica cuántica, en el mundo físico en el que vivimos, solo son observables los comportamientos cuánticos de partículas (es decir, sucesos dinámicos de rango 1, como lo llamé antes), pero que no es observable algo más allá de esto y aquí terminaría su explicación. Sin embargo, esta estructura es del mundo físico y está mostrando lo que está mostrando, una capacidad tal , que ni la más sofisticada de las máquinas ni de IA's podrían llegar a igualar jamás (o tal vez sí y este sistema lógico pueda construirse, si así fuera, le llamaría el Musitron).
Continuemos ahora con unos triángulos más que podrían llegar a formarse. Para entenderlos daré una breve explicación. Tomaré como referencia al sistema musical regular R12, por ser el más comúnmente conocido por todos, ya que es el Sistema Temperado. En el tenemos en una sola tonalidad 2048 escalas, pero se pueden agrupar entre las que comparten intervalos, es decir, la escala mayor o Modo Jónico, tiene un intervalo de Tono, Tono, Semitono, Tono, Tono, Tono, Semitono, entonces las demás escalas que tengan este intervalo se pueden agrupar con esta, por ejemplo los Modos Jónico, Dórico, Frigio, Lidio, Mixolidio, Eólico y Locrio, forman un grupo de escalas de siete intervalos y yo a eso le llamo Supraescala. Pues haciendo esto con las escalas posibles en una sola tonalidad de todos los sistemas musicales regulares tenemos el siguiente triángulo, al que podríamos llamar Triángulo UniSupraescalar:
Y este siguiente sería el Triángulo Supraescalar Delimitador (porque muestra las supraescalas posibles en todas las tonalidades posibles de todos los sistemas musicales regulares, en este caso de los primeros doce):
Bueno, voy a ir terminando este post porque se ha alargado demasiado pero no sin antes explicar por qué dije que al parecer en este sistema el 12 es como un punto de equilibrio, pero que no lo podía asegurar con total certeza porque tengo que observarlo e investigarlo más a fondo. Vamos a ver...
Si queremos construir un sistema musical regular en un instrumento con trastes, como una guitarra, algo primordial es saber el largo de escala en milímetros que tendrá nuestra guitarra desde la cejuela hasta el puente. Otra cosa primordial es saber cómo calcular el valor del intervalo del sistema musical regular y esto se hace mediante la raíz n de 2 o lo que es lo mismo 2^(1/n), siendo que la n toma el valor del sistema musical regular que vayamos a construir. Tomemos como ejemplo al sistema musical regular R12 (Temperamento Igual). Tendremos que calcular la raíz duodécima de 2 o lo que es lo mismo 2^(1/12), lo cual nos dará el valor que tiene el semitono (1,0594630943...), es decir, el valor de separación entre nota y nota, o lo que es lo mismo, el valor de sus intervalos, que son todos iguales de un semitono, ya que si afinamos una cuerda al aire en un LA(4) a 440 Hz, para saber la frecuencia de la siguiente nota tendríamos que multiplicar 440 por 2^(1/12)^1 que sería igual a la nota la#/sib con una frecuencia de 466,163 Hz y si quisiéramos saber la frecuencia de la nota sol#/lab, que es un semitono menos que el LA(4), pues multiplicaríamos 440*(1,0594630943^ -1) y nos daría 415,304 Hz. Explico todo esto porque al transportar un sistema musical regular a un instrumento con trastes, pareciera que sus intervalos no son iguales porque al ir haciendo los cálculos el primer traste se calcula con 2^(1/12) y da 1.0594630943, el segundo traste se calcula con 2^(2/12) y da 1,12246205, el tercer traste con 2^(3/12) que da 1,18920712, etcétera y parece que sus intervalos no sean iguales por esto pero si que lo son, el cálculo de la frecuencia lo demuestra, es algo enrevesado de ver pero es así, todos los intervalos son iguales y tienen el valor de un semitono que es 1,0594630943... Entonces una vez tengamos claro todo esto, lo que hay que hacer es transportar este sistema musical regular R12 al mástil de la guitarra colocando trastes en su debido lugar y eso se hace sabiendo el largo de escala, que es la medida en milímetros de una cuerda que va de extremo a extremo, esto es, de la cejuela al puente de la guitarra. Para ello se utiliza la siguiente fórmula matemática (que equivale al primer traste):
Largo de escala * (1-(1/2^(1/12)))
Los largos de escala en guitarras suelen ser de 650mm pero yo voy a hacer el largo de escala en correspondencia con el número PI. Para ello solo hay que multiplicar el número PI por 2 y después por 100, lo que nos dará un largo de escala de 628,3185307179 milímetros, que yo voy a redondear a 628 milímetros. Una vez tenemos el largo de escala listo, podemos calcular la separación de los trastes y demás. He hecho una imagen para que se vea mejor:
Y bueno aquí llega lo que nos ocupa, el por qué digo que el 12 actúa como un punto de equilibrio (aunque tengo que profundizar más en esto). Como se ve en la imagen anterior, el sistema musical regular R12 (Temperamento Igual) se está construyendo bajo una cuerda al aire que es un LA(4) a 440Hz, por eso en el traste 12 tenemos el doble de la frecuencia de 440 Hertzios, porque este sistema musical sólo tiene doce notas por lo que llaman la octava, es decir, el traste doce está mostrando la primera octava, un LA(5). Pues bien, si uno se fija bien, en la línea del traste doce tenemos al traste 12 y al número 2, lo cual podemos tomar como la raíz duodécima de dos, que es igual a 1,0594630943... La siguiente octava, LA(6) está en el traste número 24 y ahí nos aparece el 24 y el 4, lo cual podemos tomar con la raíz vigesimocuarta de 4 o 4^(1/24), que es igual a 1,0594630943... La siguiente octava, LA(7) estaría en el traste 36 y estaría acompañado por un 8, que sería la raíz trigesimosexta de 8 u 8^(1/36) que es igual a 1,0594630943... La siguiente octava, LA(8) sería el traste 48 acompañado del número 16, la siguiente octava, LA(9), sería el traste 60 acompañado del número 32, la siguiente octava, LA(10), sería el traste 72 acompañado del número 64, la siguiente octava, LA(11), sería el traste 84 acompañado del número 128 y la siguiente octava, LA(12), sería el traste 96 acompañado del número 256, llegando a ocho veces la octava (que yo llamo octavacion), es decir, el traste 96 acompañado del número 256, que sería 256^(1/96) que es igual a 1,0594630943...
Y aquí es donde viene el por qué digo que el 12 actúa como punto de equilibrio de todos los sistemas musicales regulares. Resulta que si multiplicamos 256 por 96 nos da 24576, que es el número de escalas en todas las tonalidades que tiene este sistema musical regular R12 y si hacemos 256^(1/96) nos da 1,0594630943... Cualquiera podría pensar que debe ser algo que se cumple en todos los sistemas musicales regulares al hallar ocho veces la octava del sistema musical regular que sea y que al multiplicarlo por el número que le acompaña dará el número total de escalas de ese sistema musical regular en particular, pero no es así. Es algo que sólo pasa con el sistema musical R12 (o Temperamento Igual). Es más, lo investigué, no tan a fondo como me gustaría, tengo que seguir investigándolo, pero descubrí que este sistema musical R12 actúa justamente como un punto de equilibrio entre todos estos sistemas musicales regulares posibles desde el primero hasta infinito. A continuación muestro una imagen organizando los primeros sistemas musicales regulares para investigar este asunto:
¿Por qué uso en la imagen anterior la tabla de multiplicar del 8? Porque así es como se muestra en todos los sistemas musicales regulares cuando se les busca ocho veces la octava, la secuencia que dan es la tabla de multiplicar del 8. Pero vayamos al grano. Fijémonos en el sistema regular R12, que está remarcado en color verde. A la derecha hay una columna llamada "Nombre de las Constantes" que muestra dos formas de calcular el que estos sistemas musicales tengan el mismo intervalo entre sus notas. Entonces, en el sistema R12 si hacemos la raíz 12ª de 2 obtendremos 1,0594630943 y si hacemos la raíz 96 de 256 o 256^(1/96), obtendremos también 1,0594630943 e incluso si multiplicamos 96*256 nos da 24576, que es el número total de escalas de este sistema R12 en todas sus tonalidades posibles.
Elijamos ahora otro, por ejemplo el R11 que está al lado del R12, justo por encima. Si hacemos la raíz 11ª de 2 obtendremos 1.0650410894399627 que sería el valor del "semitono" de este sistema musical regular de 11 notas por octava de intervalos iguales y necesitaríamos hacer este cálculo para armar este sistema musical de 11 notas e intervalos iguales. Si al R11 le hacemos la raíz 88 de 256 obtendremos también 1.0650410894399627, pero si multiplicamos 88*256 nos da 22528, no nos da las escalas en todas sus tonalidades posibles como sí sucedía con el R12, es más, para poder hallarlas hay que dividir entre 2.
Elijamos ahora el sistema musical R10. Si hacemos la raíz 10ª de 2 obtendremos 1.0717734625362932. Si le hacemos la raíz 80 de 256 o 256^(1/80) obtendremos también 1.0717734625362932, pero si multiplicamos 80*256 nos da 20480, es decir, tampoco sucede lo mismo que con el R12, porque las escalas totales en todas las tonalidades de este sistema musical R10 son 5120. Esta vez, para poder hallar las escalas en todas las tonalidades posibles de este sistema musical R10, hay que dividir 20480 entre 4.
No vayamos ahora con el sistema musical regular R9, en vez de eso comprobemos qué sucede con el R13. Si hacemos la raíz 13ª de 2 obtendremos 1.0547660764816467, que sería el valor del "semitono" de este sistema musical regular de 13 notas por octava de intervalos iguales y necesitamos hacer este cálculo para armar este sistema musical de 13 notas e intervalos iguales. Si al R13 le hacemos la raíz 104 de 256 o 256^(1/104), obtendremos también 1.0547660764816467, pero si multiplicamos 104*256 nos da 26624, no nos da las escalas en todas sus tonalidades posibles como sí sucedía con el R12, de hecho esta vez está dando incluso menos escalas, porque las escalas en todas las tonalidades posibles de este sistema musical R13 son 53248. Esta vez, al ir un sistema musical regular más allá del R12 hay que multiplicar esas 26624 por 2. Con el R14 habría que multiplicar por 4, con el R15 por 8, con el R16 por 16, con el R17 por 32, etcétera.
Y esto es lo que sucede. Parece ser que de entre todos estos sistemas musicales regulares, el R12 actúa como punto de equilibrio entre todos ellos. De hecho , si uno se fija bien, está tan en equilibrio que incluso las escalas posibles en una sola tonalidad del R12 está incluso marcando al primero de los sistemas musicales regulares. La siguiente imagen aclarará mejor a qué me refiero:
Y bueno, aquí va a terminar este post. El otro día encontré unos apuntes antiguos míos del año 2013 sobre las observaciones que iba haciendo, eran sólo sobre el Sistema Temperado (que ahora llamo R12) y allí decía que para mi era muy obvio que estaba en estrecha relación con los vértices interiores de un cuboctaedro, pero confiado de mi no anoté el por qué y lo olvidé, e incluso en el logo de este blog está allí el cuboctaedro, apenas inapreciable, pero uno lo puede ver si acerca la vista lo suficiente. Me intriga bastante aquella observación que hice, porque no es que el árbol me impidiera ver el bosque, sino que observando aquel árbol me acerqué bastante a describir el bosque. ¿Cómo lo hice? Ni idea, me arrepiento de no haberlo apuntado. Aún así, la observación que hago el día de hoy, me podría llevar más allá aún de ver el árbol y el bosque, es decir, no es ya solamente sobre el sistema musical R12 que hice en el 2013, sino sobre todos estos sistemas musicales de intervalos iguales (que ahora llamo Rn, de regulares), que describen un tetraedro dentro de un cubo (para simplificarlo en tres dimensiones geométricas y que nos entendamos, porque en realidad parece ser que lo describen en una cuarta dimensión geométrica ya que siguen las secuencias de un hipercubo), pero en el núcleo del tetraedro hay posiblemente un octaedro (que precisamente es la conjugación de un cubo y también es el núcleo de un triángulo de Sierpinski tridimensional, sí, el que aparece en el Triángulo de Pascal). Es curioso que ya en el 2013 dijera que el R12 estaba en estrecha relación con un cuboctaedro, porque este último puede transformarse en un tetraedro y un octaedro (es decir, puede ser el núcleo del octaedro dentro del cubo o ser el mismo cuboctaedro transformado en octaedro según necesite, además a esto se le ha de sumar lo del 12 en equilibrio que acabamos de ver sobre todos los sistemas musicales regulares y además el cuboctaedro en 4 dimensiones geométricas está conectado al 24-cell, la complejidad aumenta, es como si estas formas geométricas se acoplaran unas con otras formando un todo hipercomplejo, pero tiene sentido que un cuboctaedro "intermedie", porque aunque esté observando solamente la estructura de sistemas musicales regulares, me doy cuenta que también es la misma estructura para sistemas musicales irregulares y hasta ahora tenía sentido que sólo aparecieran politopos regulares como el cubo y el tetraedro, pero el cuboctaedro no es un politopo regular aunque puede transformarse en uno). En fin, mejor dejarlo aquí que ya se alargó demasiado este post. El otro día también, cuando iba caminando por la calle, había un músico tocando y mientras lo escuchaba y me iba alejando pensé... "¿¡En serio esto es un tetraedro dentro de un cubo!? ¡Que tendrá que ver!" y me hizo gracia que yo mismo, en ese mismo momento, no encontrara relación alguna entre la música que escuchaba del músico callejero y la estructura de un tetraedro dentro de un cubo. Pero después, poniéndome a observar de nuevo toda esta estructura de los sistemas musicales regulares, pienso... "¡Sin duda es un tetraedro dentro de un cubo!". ¿Estaré loco? Y tal vez muchos piensen que lo estoy, porque cuando oigan a un músico tocar, les pasará igual que a mi me pasó y les será difícil encontrar la relación entre esa música que escuchan y la estructura de un tetraedro dentro de un cubo. A ellos les va esta pregunta que yo mismo me hice: ¿desde cuándo puedes pensar con el oído?
ACTUALIZACIÓN:
Si lo de antes te pareció loco, será mejor que no leas esto siguiente y mucho menos si no has leído algo sobre filosofía metafísica o si no estás dispuesto a abrirte a más disciplinas y no solo especializarte en una sola, como podría ser matemáticas o geometría o cualquier otra, puesto que cuanto más se especializa uno en una materia o disciplina, tanto más les impide ver el conjunto de las otras.
Las evidencias que he encontrado por el momento apuntan a que lo que genera a esta estructura del tetraedro dentro de un cubo (es decir "lo que piensa" a esta estructura) tiene todas las papeletas de ser un cristal-metafluido polimorfico que posee todas las propiedades a un mismo tiempo, de entre ellas que es sólido, liquido y gaseoso, todo al mismo tiempo, pero no es de este universo físico, sino que es lo que genera a este universo físico, yo no puedo demostrarlo mediante la experimentación y seguramente nadie pueda pues estoy casi convencido que para "saludar" a este cristal-metafluido polimorfico habría que adentrarse dentro de un agujero negro, justo el que está en el centro de las galaxias generando y destruyendo estrellas, pero cuando esa especie de cristal-metafluido polimorfico separa su mundo metafísico de este universo físico es por algo vital (si es que eso es algo que haga dicho cristal-metafluido polimorfico, porque no descarto que lo pueda hacer algún que otro ente metafísico). Esto me rondaba esto dos días por la cabeza y pensaba ya haber alcanzado la locura máxima, pero investigando el asunto vi que estaba relacionado con el condensado de Bose-Einstein y que además se hizo un experimento no hace mucho y dio lo que llamaron el quinto estado de la materia.




































0 comentarios:
Publicar un comentario